「深入理解计算机系统」学习笔记(第二章)
本文主要是《深入理解计算机系统》第二章(信息的表示和处理)的学习笔记。主要依据 B 站 UP 主九曲阑干对 CSAPP 的 中文讲解。
本章主要涉及如下知识点:
- 信息存储
- 整数表示
- 整数运算
- 浮点数
信息存储
在计算机中,内存可以视为一个大数组,数组的元素由一个个字节组成。每一个字节都由一个唯一的数字表示,称为地址。地址的集合称为 虚拟地址空间。
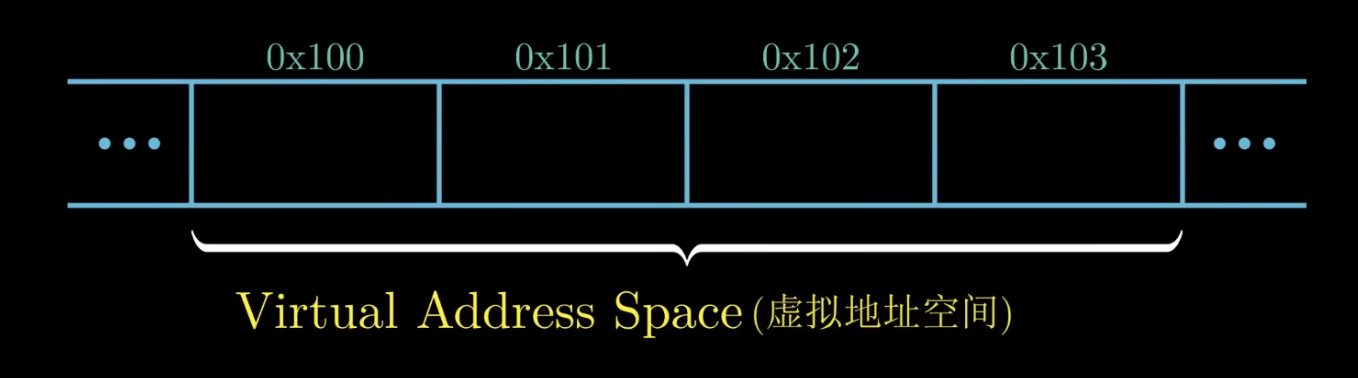
字节
一个字节是由 8 个位组成,一个位的取值只为 0 或 1。
| 二进制 | 十进制 |
|---|---|
00000000 | 0 |
11111111 | 255 |
我们将使用二进制表示数字的方式称为 位模式。
十六进制
因为使用二进制表示比较冗长,而十进制与二进制之间的转换较为麻烦。所以引入了十六进制。
十六进制使用 10 个数字(0123456789)和 6 个字母(ABCDEF)表示。
在 C 语言中,使用 0x 开头表示一个十六进制。
| 十进制 | 十六进制 | 二进制 |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
字长
字长决定了虚拟地址空间最大值。
| 字长 | 虚拟地址空间 | 备注 |
|---|---|---|
| w 位 | 0 ~ \(2^w-1\) | |
| 32 位 | 0 ~ \(2^{32}-1\) | 4GB |
| 64 位 | 0 ~ \(2^{64}-1\) | 16EB |
C 语言各个数据类型大小如下表所示:
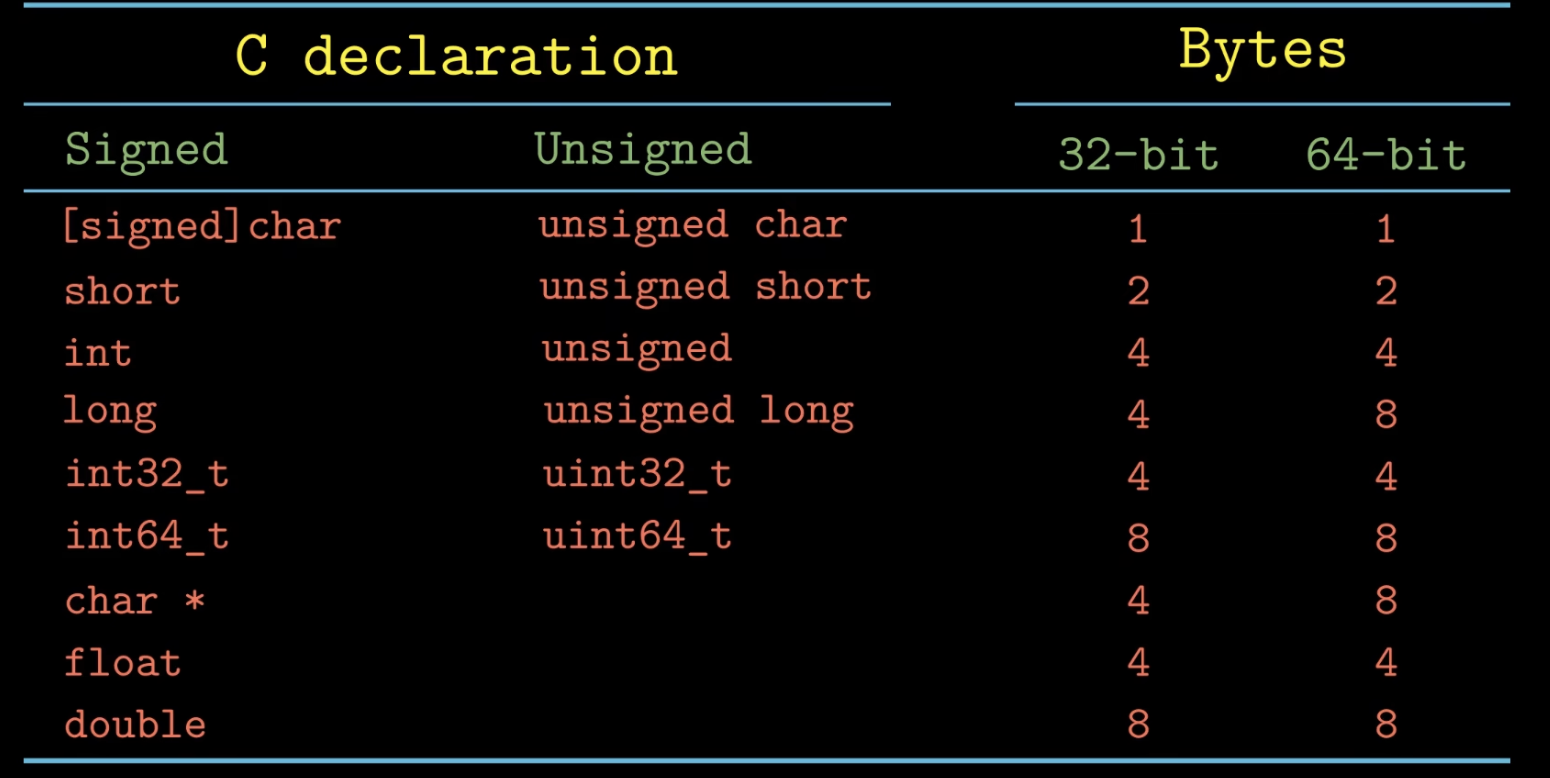
地址和字节排布
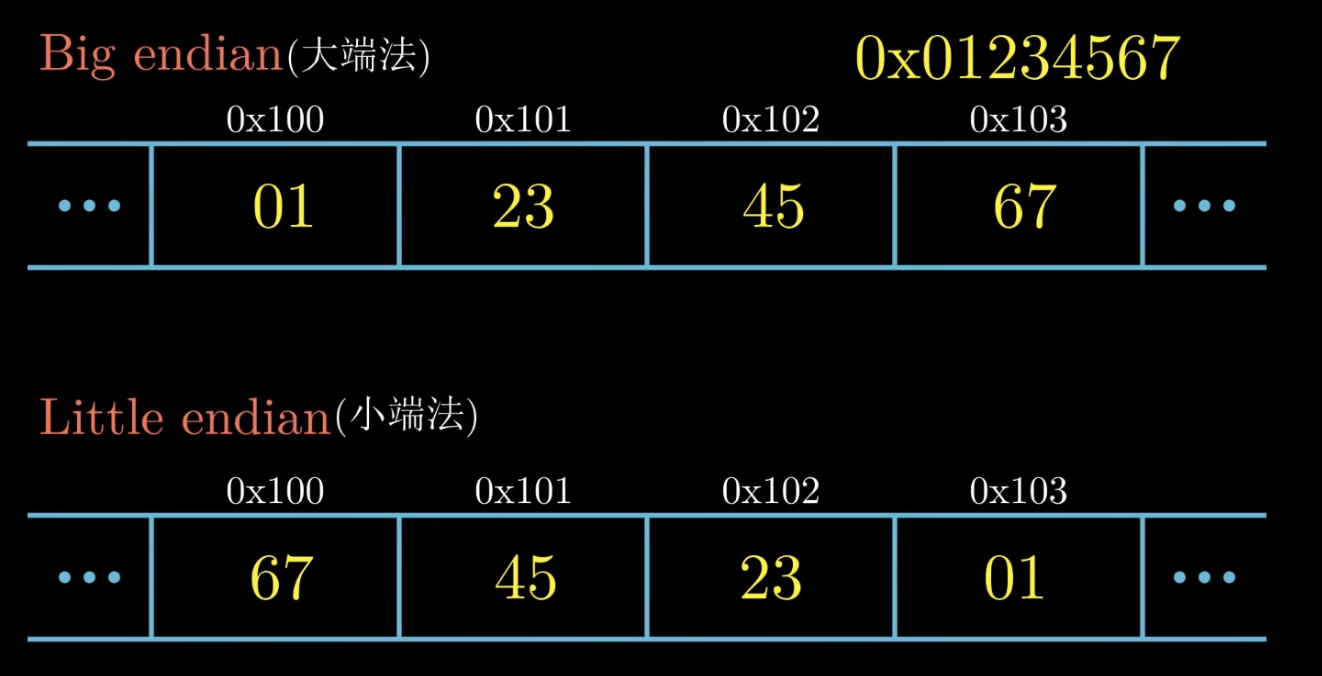
目前,大部分使用的 PC 机使用小端法排布。
字符串表示
C 语言中字符串被定义为以 NULL 结束的字符数组。例如,字符串 abcde 虽然只有 5 个字符,但长度为 6。
1 | const char *s = "abcde"; |
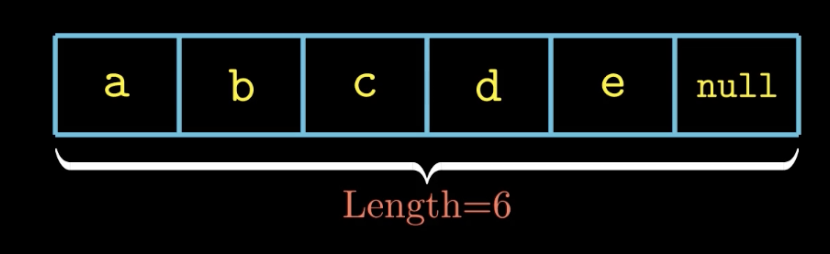
NULL 在 C 语言中对应 0x00,该字符串在内存中以十六进制表示为:
1 | 61 62 63 64 65 00 |
C 语言的位级运算
逻辑非:
| ~ | |
|---|---|
| 0 | 1 |
| 1 | 0 |
逻辑与:
| & | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
逻辑或:
| 0 | ||
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
逻辑异或:
| ^ | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
C 语言的逻辑运算
逻辑运算中,所有非 0 都表示 true,0 表示 false。
| 表达式 | 结果 | 备注 |
|---|---|---|
| 0x41 | 0x00 | |
| !0x00 | 0x01 | |
| !!0x41 | 0x01 | |
| 0x69 && 0x55 | 0x01 | |
| 0x69 | 0x55 | |
| a && 5 / a | 当 a 为 0 时,不继续判断 5 / a |
C 语言的移位运算
对于二进制数 01100011,
左移一位:11000110
左移两位:10001100
逻辑右移丢弃最右端 n 位,并在最左端补 n 个 0。
算术右移当最高位为 0 时,右移且在最左端补 0;最高位为 1 时,在最左端补 1。
大部分编译器对于有符号数采用算术右移,对于无符号数采用逻辑右移。
整数表示
C 语言支持多种整型数据类型,以 64 位操作系统为例。
| C 数据类型 | 最小 | 最大 | 字节 |
|---|---|---|---|
char | \(-2^7\) | \(2^7-1\) | 1 |
unsigned char | 0 | \(2^8-1\) | 1 |
short | \(-2^{15}\) | \(2^{15}-1\) | 2 |
unsigned short | 0 | \(2^{16}-1\) | 2 |
int | \(-2^{31}\) | \(2^{31}-1\) | 4 |
unsigned int | 0 | \(2^{32}-1\) | 4 |
long | \(-2^{63}\) | \(2^{63}-1\) | 8 |
unsigned long | 0 | \(2^{64}-1\) | 8 |
int32_t | \(-2^{31}\) | \(2^{31}-1\) | 4 |
uint32_t | 0 | \(2^{32}-1\) | 4 |
int64_t | \(-2^{63}\) | \(2^{63}-1\) | 8 |
uint64_t | 0 | \(2^{64}-1\) | 8 |
需要特别注意,long 类型取值范围与机器字长有关。在 32 位机器上,long 为 4 字节;在 64 位机器上,long 为 8 字节。
无符号数编码
对于向量 \(x = [x_{w-1}, x_{w-2}, \cdots, x_1, x_0]\),
\(B2U_w(x) = x_{w-1}\cdot 2^{w-1} + x_{w-2}\cdot 2^{w-2} + \cdots + x_1\cdot 2^1 + x_0\cdot 2^0 = \sum^{w-1}_{i=0}{x_i2^i}\)
补码编码
对于向量 \(x = [x_{w-1}, x_{w-2}, \cdots, x_1, x_0]\),
\(B2T_w(x) = x_{w-1}\cdot -2^{w-1} + x_{w-2}\cdot 2^{w-2} + \cdots + x_1\cdot 2^1 + x_0\cdot 2^0 = -x_{w-1}\cdot 2^{w-1} + \sum^{w-2}_{i=0}{x_i2^i}\)