图论——拓扑排序

发表于 分类于 ，

在现实生活中，我们要做一系列的事情。而这些事情之间会存在顺序或依赖关系，即做一件事情之前，我们必须先做好另一件事。比如，在大学里学习的课程，通常都会有先后顺序。

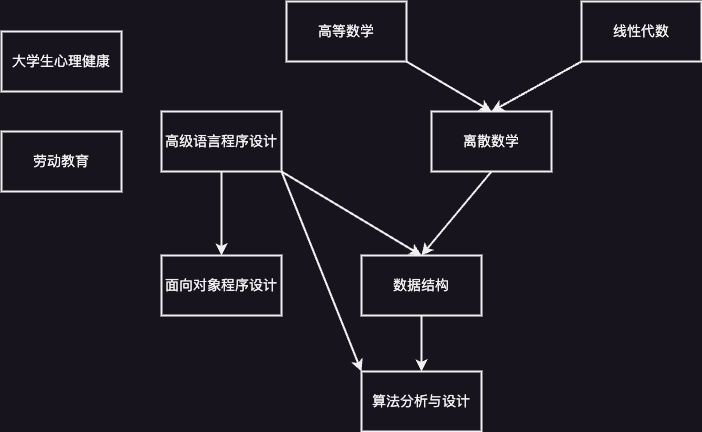
图中，“高等数学”、“线性代数”是“离散数学”的先修课程，“离散数学”、“高级语言程序设计”是“数据结构”的先修课程，“高级语言程序设计”是“面向对象程序设计”的先修课程，“数据结构”、“高级语言程序设计”是“算法分析与设计”的先修课程。而“大学生心理健康”、“劳动教育”则作为独立的课程存在，不作为先修课程。

这张课程的关系图，我们可以将其课程名称由编号代替，进而形成一张图：

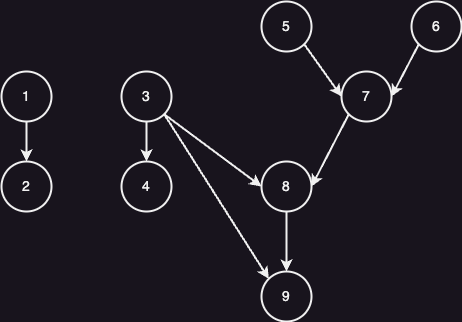
该图其中一个拓扑序列为 1 3 5 6 2 4 7 8 9。（这里之所以说是其中的一个拓扑序列，是因为一张图可以有多个拓扑序列）

继续使用课程举例，如果“课程1”依赖了“课程2”，“课程2”依赖了“课程3”，而“课程3”又依赖了课程“1”，那么无论如何我们都是无法学习的。

这种现象按照图论的说法称为“回路”。一个图有拓扑排序的条件是不能构成回路。因此，拓扑排序同时可以判断是否存在环。

拓扑排序的概念

拓扑排序是指在一个 有向无环图（DAG，Directed Acyclic Graph）中，我们将定点以线性的方式进行排序，使得任意一对由 \(u\) 指向 \(v\) 的有向边 \((u,v)\)，都有 \(u\) 在 \(v\) 的前面。

拓扑排序的目标是将所有节点排序，使得排在前面的节点不能依赖于排在后面的节点。

Kahn 算法（基于 BFS 的拓扑排序）

Kahn 算法是求解拓扑排序的一个十分常见的算法。其算法流程如下：

  1. 找到所有入度为 0 的点，放入队列。这些点没有先后关系，可任意输出。
  2. 弹出队头元素 \(t\)，将 \(t\) 的所有邻接点的入度减 1。如果有的点入度为 0，则将其加入队列。
  3. 不断执行以上步骤，直至队列为空。如果队列为空后仍然有点没有入队，则该图不是一个 有向无环图，不存在拓扑排序。

上面课程表的一个拓扑序列为 1 -> 3 -> 5 -> 6 -> 2 -> 4 -> 7 -> 8 -> 9

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <bits/stdc++.h>
using namespace std;
int main() {
  int n, k;
  cin >> n >> k;
  vector<vector<int>> a(n + 1);  // 邻接表
  vector<int> ind(n + 1, 0);     // 入度
  for (int i = 0; i < k; ++i) {
    int u, v;
    cin >> u >> v;
    ind[v]++;
    a[u].push_back(v);
  }
  queue<int> q;
  for (int i = 1; i <= n; ++i) {
    if (!ind[i]) {
      q.push(i);
    }
  }
  vector<int> ord(n);  // 存储拓扑排序
  int idx = 0;
  while (q.size()) {
    int tt = q.front();
    q.pop();
    ord[idx++] = tt;
    for (int& i : a[tt]) {
      // 为其邻接点入度减 1
      ind[i]--;
      if (!ind[i]) {
        q.push(i);
      }
    }
  }
  if (idx != n) {
    puts("Circle!");
  } else {
    for (int i = 0; i < n; ++i) {
      cout << ord[i] << " \n"[i == n - 1];
    }
  }
}