图论——存储图

发表于 更新于 分类于 ，

图论算法是一个很大的专题，有很多的知识点。但是，在学习图论的各个知识点之前，首先需要对于图的存储有十分清楚的理解，了解各种方式的优劣。

一般而言，图的存储方式有 4 种：

  • 直接存边
  • 邻接矩阵
  • 邻接表
  • 链式前向星

直接存边

在某些算法中（如用于解决最小生成树问题的 Kruskal 算法），我们可以直接将边存在一个结构体中。这种方式的优势是编码快速，空间效率高，并且便于依据边权进行排序。

结构体的定义如下：

1
2
3
4
5
struct Edge {
  int u;  // 起点
  int v;  // 终点
  int w;  // 边权
};
uvw
013
125
214
268
459

建立上表中图并排序的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<Edge> edges;
edges.push_back({0, 1, 3});
edges.push_back({1, 2, 5});
edges.push_back({2, 1, 4});
edges.push_back({2, 6, 8});
edges.push_back({4, 5, 9});

sort(edges.begin(), edges.end(), [&](Edge a, Edge b) {
  return a.w > b.w;
});
for (Edge &edge : edges) {
  printf("%d %d %d\n", edge.u, edge.v, edge.w);
}
// 4 5 9
// 2 6 8
// 1 2 5
// 2 1 4
// 0 1 3

邻接矩阵

邻接矩阵是 3 种存储方式中最为简单的方式。本方式使用一个二维数组 g[N][N] 进行图的存储。

其中，g[i][j] = w 代表点 i 至点 j 存在一条边权为 w 的有向边。当然，如果仅仅想表示 i 和 j 之间有边，可以将 w 定为任何值。一般而言，如果使用邻接矩阵表示边权时，通常使得该邻接矩阵所有元素的初始值为 INF（一个十分大的数字）；使用邻接矩阵表示有边时，可以直接将该邻接矩阵定义为 二维布尔数组。

使用邻接矩阵的空间复杂度为 \(O(n^2)\)。

注意：无向图是特殊的有向图。节点 i 至节点 j 有一条无向边代表节点 i 和节点 j 之间，以及节点 j 和节点 i 之间分别有条有向边。

例如，一个 1000 个节点的图，点的编号从 1 开始，可以为该邻接矩阵定义为 g[1001][1001]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int INF = 0x3f3f3f3f;    // 使用 INF 代表一个十分大的数字
int g[1001][1001];

void add_direct(int u, int v, int w) {
  g[u][v] = min(g[u][v], w);   // 如果有重边，则将其赋值为较小的值
}

void add_undirect(int u, int v, int w) {
  g[u][v] = g[v][u] = min(g[u][v], w);
}

int main() {
  memset(g, 0x3f, sizeof(g));  // 使用 memset 将 g 数组所有元素赋为极大值
  add_direct(100, 200, 30);    // 添加一条 100 -> 200 的有向边，边权为 30
  add_undirect(500, 600, 80);  // 添加一条 500 <-> 600 的无向边，边权为 80
}

邻接矩阵优点：

  • 编程简单；
  • 查找快速，复杂度仅为 \(O(1)\)；
  • 十分适合稠密图；

邻接矩阵缺点：

  • 不适合稀疏图。当使用邻接矩阵表示稀疏图时，会有大片的空间浪费；
  • 不能够存储重边。

邻接表

为了解决邻接矩阵浪费空间的问题，可以使用邻接表。邻接表是一个类似于链表的结构。邻接表的空间复杂度为 \(O(n+m)\)。

例如，一个节点个数为 7 的有向图，可以有如下边：

uvw
013
125
214
268
459

其实现后效果可以如下图所示：

使用 STL 中的 vector 容器实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
const int N = 7;
struct Edge {
  int v, w;
};
vector<Edge> e[N];  // 使用 vector 数组下标代表 u
void add_edge(int u, int v, int w) {
  e[u].push_back({v, w});
}
int find(int u, int v) {
  for(int i = 0; i < e[u].size(); i++) { // 遍历所有由 u 开始的边
    if (e[u][i].v == v) {
      return e[u][i].w;
    }
  }
  return 0x3f3f3f3f;    // 找不到，则输出个极大值
}
int main() {
  add_edge(0, 1, 3);
  add_edge(1, 2, 5);
  add_edge(2, 1, 4);
  add_edge(2, 6, 8);
  add_edge(4, 5, 9);

  int w1 = find(1, 4);  // 找不到边，返回 0x3f3f3f3f
  int w2 = find(0, 1);  // 找到该边，返回 3
}

链式前向星

链式前向星是空间效率最高的存储方式。其使用静态数组来存储边，来模拟邻接表。

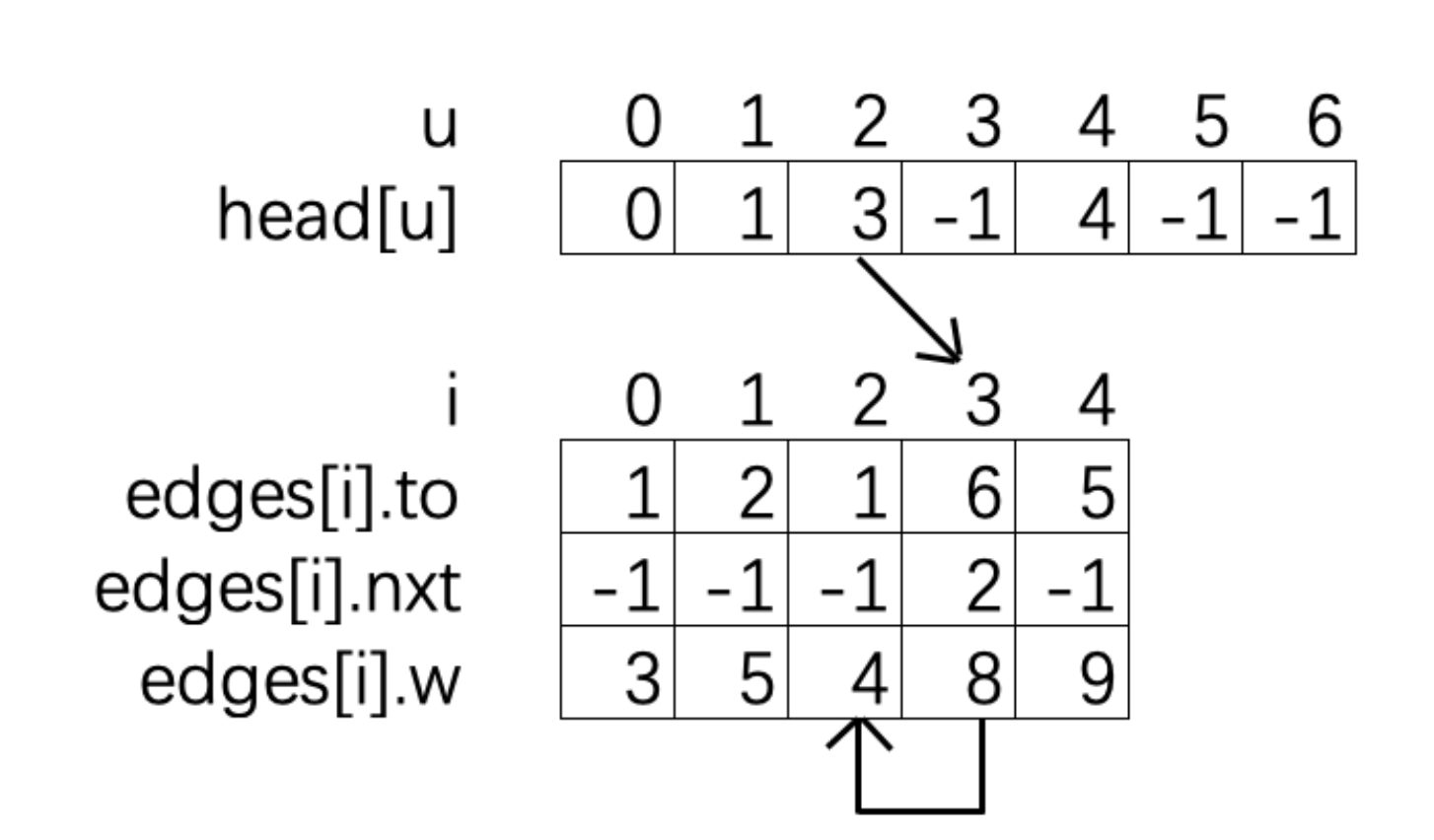
链式前向星使用 head[N] 来确定头节点，使用 edges[M] 来表示边。边的类型是个结构体，其中包括 to（指向的边）、nxt（下一条边）、w（边权）。

依然使用上面邻接表的例子。使用链式前向星，其空间存储如下图所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
const int N = 1e5 + 10; // 最多有 100,000 条边
const int M = 1e6 + 10; // 最多有 1,000,000 条边
struct {
  int to, nxt, w;
} edges[M];
int head[N], cnt;
void add(int u, int v, int w) {
  edges[cnt].to = v;        // 指向 v 点
  edges[cnt].w = w;         // 边权为 w
  edges[cnt].nxt = head[u]; // 将 u 的邻接点向后顺延
  head[u] = cnt++;
}
int find(int u, int v) {
  for(int i = head[u]; ~i; i = edges[i].nxt) { // ~i 相当于 i != -1
    if (edges[i].to == v) {
      return edges[i].w;
    }
  }
  return 0x3f3f3f3f;
}

int main() {
  memset(head, -1, sizeof(head));  // 初始化
  add(0, 1, 3);
  add(1, 2, 5);
  add(2, 1, 4);
  add(2, 6, 8);
  add(4, 5, 9);

  int w1 = find(1, 4);  // 找不到边，返回 0x3f3f3f3f
  int w2 = find(0, 1);  // 找到该边，返回 3
}