菜狗学算法——基础知识
算法(Algorithm)是用来解决问题的方法。对于相同的问题,使用不同的算法,可能得到的结果是相同的,但在其背后所消耗的资源(时间、空间)也许千差万别。
二分查找
还记得 CS50 撕书教授 David 撕电话薄的视频吗?


在该视频中,David 想要在电话薄中查找自己的姓名。他每次将电话薄从中间撕开,判断其姓名首字母D在该页的前面还是后面,丢掉无用的部分。这段视频生动的展示了「二分查找(Binary Search)」这种算法。
那么,二分查找究竟解决了什么痛点?
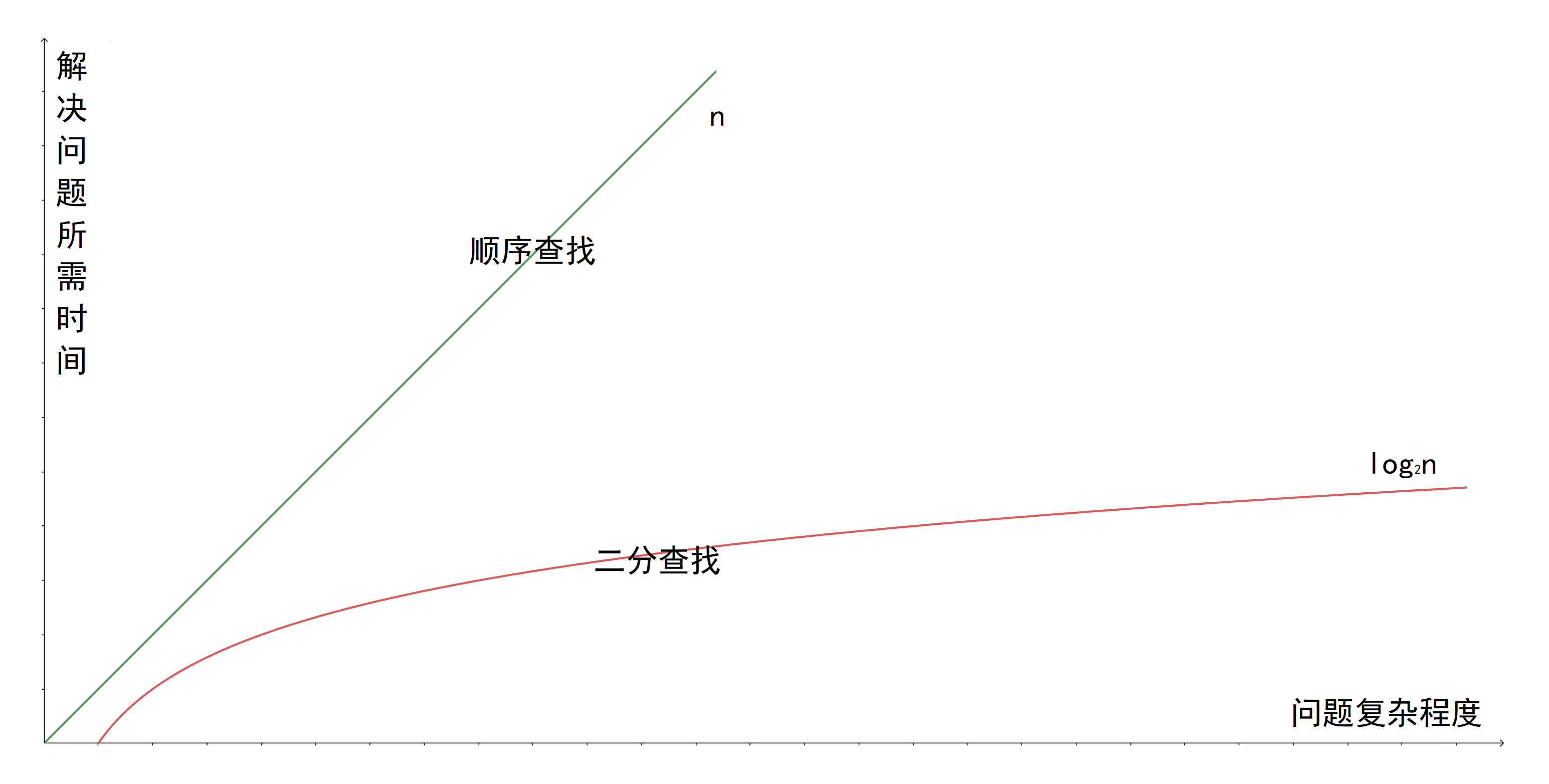
使用顺序查找(Linear Search)时,我们可能从前往后找所需的一个数据。
仍然以电话簿为例。假如整本电话薄有 1024 页,你最多需要找 1024 次才能找到你所需要的姓名。
而使用二分查找时,你最多只需要寻找 \(log_2 1024 = 10\) 次就可以找到你所需要的姓名。
如上所示的两种查找方式的时间增长趋势如下图:
运行时间
大 O 表示法
运行时间(Running time)指一个算法执行所用的时间。有许多方式可以代表运行时间,其中最为广泛的是「大_O_表示法」。它使用斜体的_O_来表示。大_O_表示法表示了一个算法最差的情况所需的运行时间。
上面所示的增长趋势用大_O_表示法可以为以下图像:
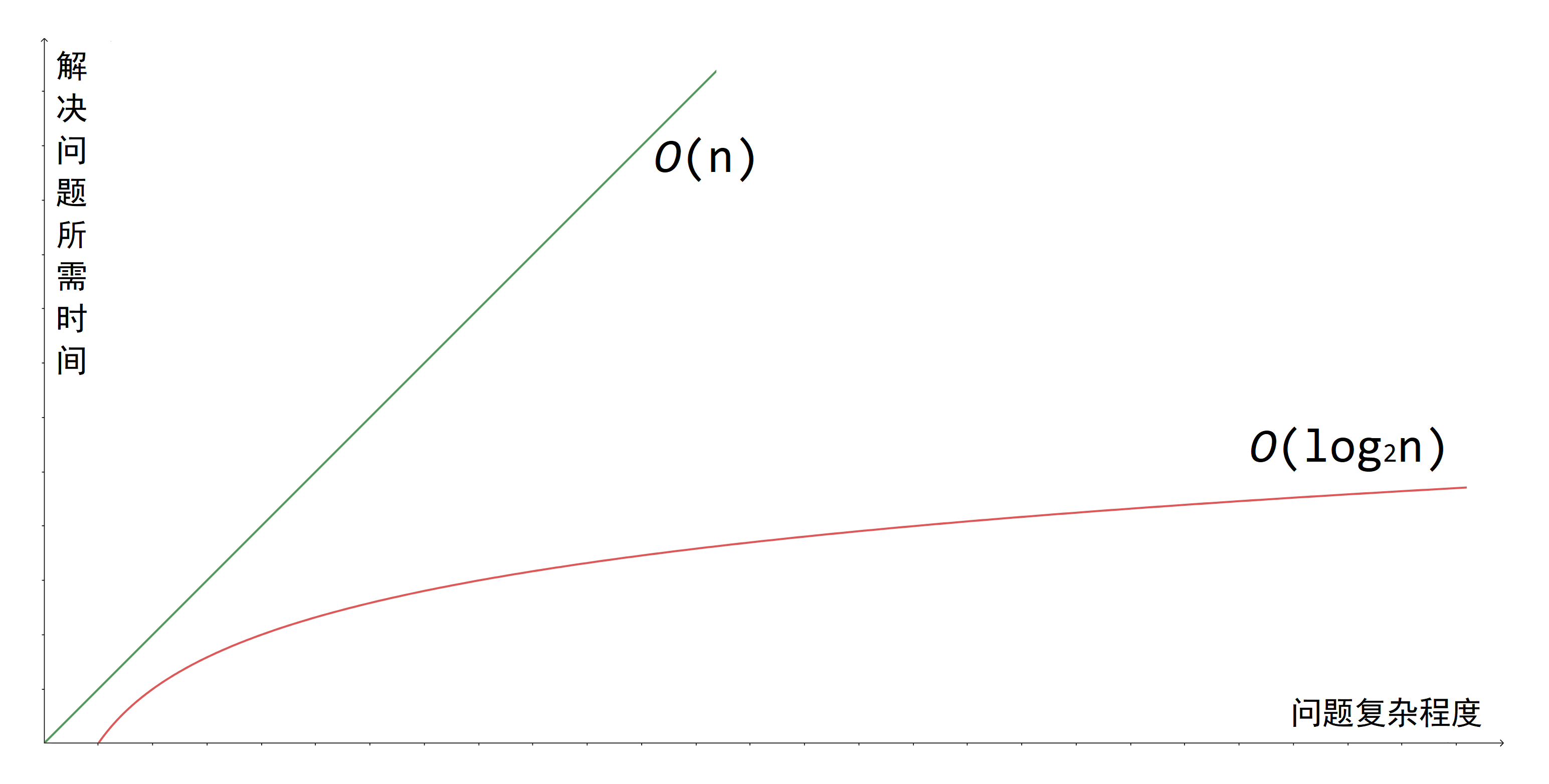
为了表示某一算法的增长趋势,通常我们会省略一些东西(例如系数、底数等),故以上图像可以再次优化:
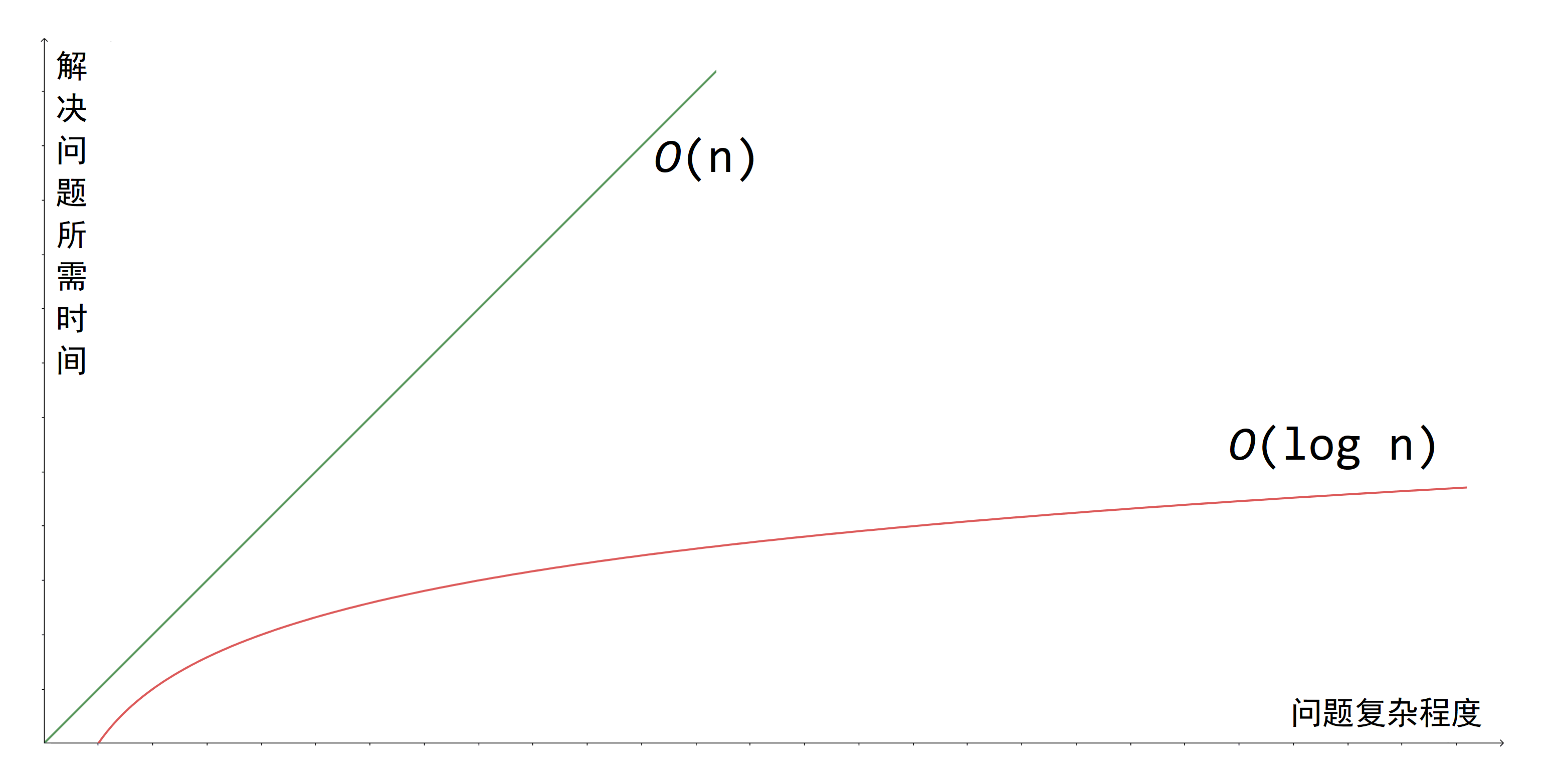
下面列举几个常见的大_O_表示法的表现形式:
- O(\(n^2\))
- O(n log n)
- O(n) (如顺序查找)
- O(log n) (如二分查找)
- O(1)
大 Ω(Omega) 表示法
与大_O_表示法相反,大 Ω 表示法表示了最好的情况。
下面列举几个常见的大_Ω_表示法的表现形式:
- Ω(\(n^2\))
- Ω(n log n)
- Ω(n)
- Ω(log n)
- Ω(1) (如顺序查找、二分查找)